Diffracting molecules at a standing light wave
Diffracting molecules at a standing light wave
Since the early beginnings of QNP, our group has been dedicated to exploring new optical elements that can serve in the coherent manipulation of complex, polarizable or even polar molecules. This is why we started molecule diffraction at an optical phase grating [1], made from a retro-reflected laser beam.
Similar ideas had been explored with atoms before, where the interaction of atoms with a narrow or extended grating has become known as Kapitza-Dirac [2] and Bragg [3] diffraction and were first shown in the Pritchard group at MIT.
When an atom or molecule enters the grating, it is polarized by the electric field of the laser wave. The resulting dipole moment then also interacts with the electric field. In consequence, thede Broglie wave accumulates a phase during the transit, which varies spatially with the grating period.
This mechanism differs from the original proposal by Kapitza and Dirac for the diffraction of electrons [4] which is based on poinderomotive potentials and which has been first demonstrated by the Batelaan group in Lincoln/Nebraska in 2001 [5].
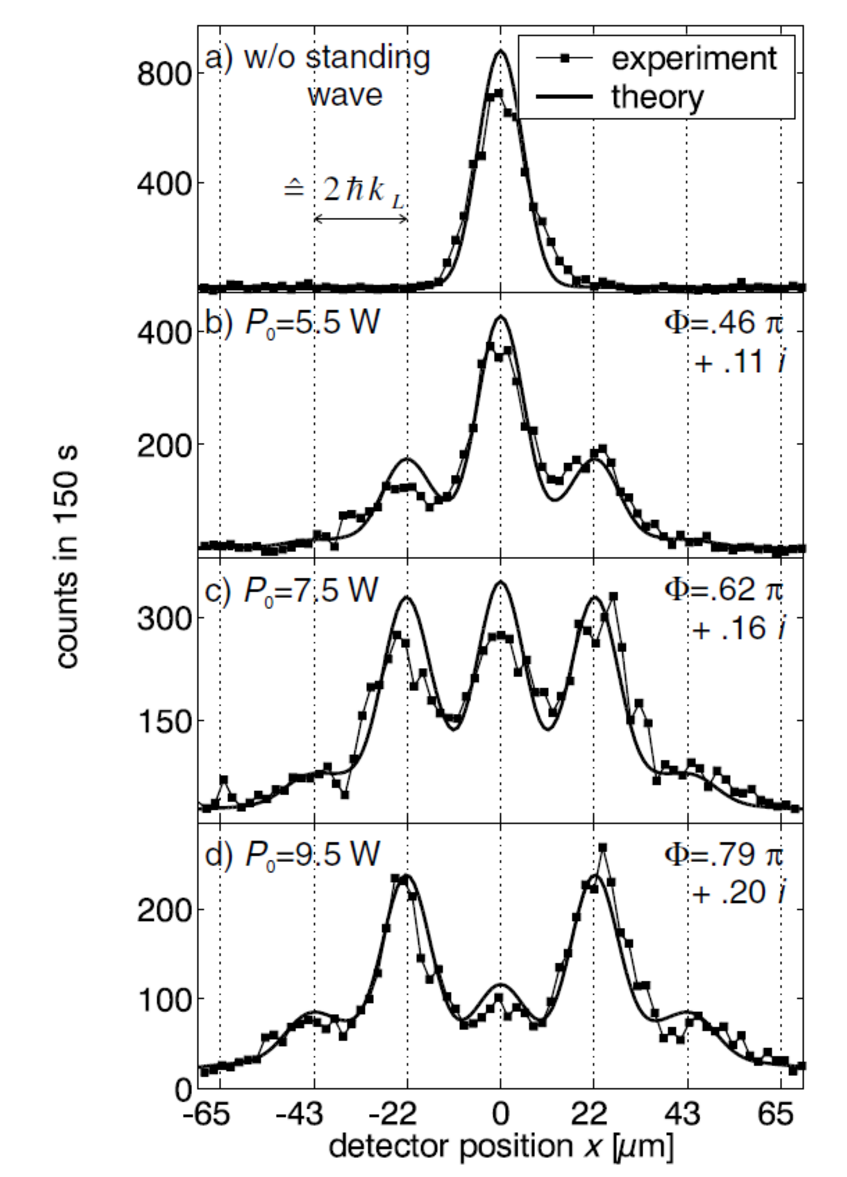
Kapitza Dirac diffraction of fullerenes
At low laser power, the far-field diffraction pattern resembles the one behind a nanomechanical grating and peaks in the central fringe. However, at high laser power the phase shift becomes large enough to populate higher diffraction orders and to suppress the zeroth order peak.
Bragg diffraction of polar molecules, the case of antibiotic cyprofloxacin
Optical standing light waves overcome the limitations of nanomechanical gratings. They are perfectly defined, cannot be destroyed, are tunable in situ, ultra-high vacuum compatible and they give no room for van der Waals forces. Because of this, they allow diffracting polar molecules which have shown dephasing interactions in passing through nanomechanical masks.
Photodepletion gratings
While phase gratings provide a modulation of the de Broglie wave with 100% transmission, photodepletion gratings are required to impose the Heisenberg trick, i.e. establishing spatial coherence from an initially incoherent field. Also in the detection process, photodepletion gratings are important. They have become the essence of MUSCLE and (BI)OTIMA interferometry.
References
- K. Simonović, R. Ferstl, A. Di Silvestro, M. Mayor, L. Martinetz, K. Hornberger, B.A. Stickler, C. Brand, M. Arndt, Diffracting molecular matter-waves at deep-ultraviolet standing-light waves, Phys. Chem. Chem. Phys. 26, 27617 (2024).
- C. Brand, F. Kialka, S. Troyer, C. Knobloch, K. Simonovic, B.A. Stickler, K. Hornberger, M. Arndt, Bragg diffraction of large organic molecules, Phys Rev Lett 125, 033604 (2020).
- O. Nairz, B. Brezger, M. Arndt, A. Zeilinger, Diffraction of complex molecules by structures made of light. Phys. Rev. Lett. 87, 160401 (2001)
- P.J. Martin, P.L. Gould, B.G. Oldaker, A.H. Miklich, D.E. Pritchard, Diffraction of Atoms Moving Through a Standing Light Wave, Phys. Rev. A 36, 2495 (1988).
- P.E. Moskowitz, P.L. Gould, S.R. Atlas, D.E. Pritchard, Diffraction of an Atomic Beam by Standing-Wave Radiation, Phys. Rev. Lett. 51, 370 (1983).
- P.L. Kapitza, P.A.M. Dirac, The Reflection of Electrons from Standing Light Waves, Proc. Camb. Philos. Soc. 29, 297 (1933).
- D.L. Freimund, K. Aflatooni, H. Batelaan, Observation of the Kapitza-Dirac Effect, Nature 413, 142 (2001).
